Ejemplo: algoritmo método de Newton

A continuación escribimos un ejemplo sencillo para ilustrar la implementación en C del método de Newton.

#include <stdio.h>
#include <math.h>

double f(double x){
    // Aquí definiremos la función con la que queremos trabajar
    // En este caso: $f(x) = x^4 - x^2 -x$.
    return pow(x,4)-pow(x,2)-x;
}

double fDerivada(double x) {
    // Aquí definimos la derivada de la función anterior
    return 4*pow(x,3)-2*x-1;
}

int main(void) {
    double x;
    int maximaIteracion;
    printf("PRIMER ACERCAMIENTO A LA PROGRAMACIÓN DEL MÉTODO DE NEWTON\n");
    printf("Introduce una primera aproximación, $x_0$, del cero de la función: ");
    scanf("%lf",&x);
    printf("Introduce el número máximo, $N$, de iteraciones a realizar: ");
    scanf("%i",&maximaIteracion);
    int iter = 0;
    // Método de Newton
    while (iter < maximaIteracion) {
        x = x - f(x)/fDerivada(x);
        iter++;
    }
    printf("\nSolución aproximada: x = %lf\n", x);
    double y = f(x);
    printf("\n¿Es f(x)=0?... f(x)=%lf (más exactamente: %.15g)\n", y, y);
    return 0;
}

¿Cómo puedo ejecutar este programa?

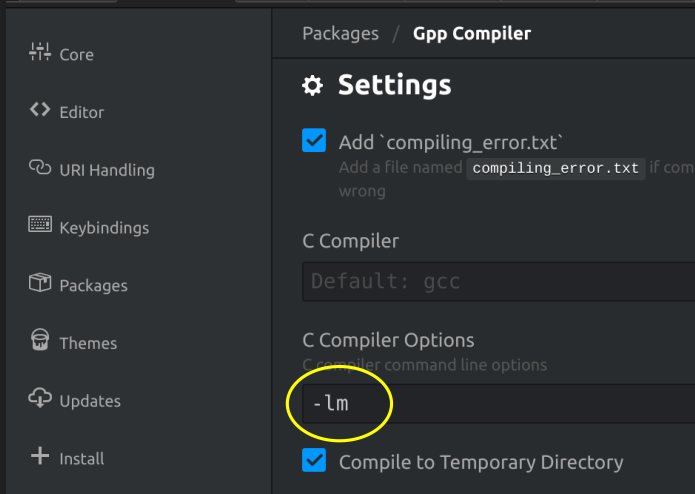
Como se puede ver, el programa utiliza la biblioteca matemática estándar math.h (que contiene funciones como pow, cos, exp, etc). Con el compilador gcc, puedes utilizar la opción -lm para enlazar el programa con esta biblioteca. Si usas el editor Atom y el paquete gpp-compiler, deberás acceder a la configuración de este paquete y, en la opción C Compiler Options, escribir -lm.

Si te interesa el uso de la terminal: para compilar el programa basta escribir la orden:

gcc -o newton newton.c -lm

Por supuesto, la orden anterior supone que el código está en el fichero newton.c y que te has situado en el directorio que lo contiene (cd <ruta_al_directorio>). La orden generará un programa llamado newton, que podrás ejecutar en la terminal escribiendo:

./newton

¿Qué resultados puedo esperar si ejecuto el programa?

La función introducida es un polinomio de grado $4$, $f(x)=x^4-x^2-x$, por lo que como máximo tendremos $4$ ceros.

• Una de las raíces (una de las «soluciones exactas» de nuestro problema) está clara: $x=0$. El programa te devolverá este resultado si la inicialización es pequeña en valor absoluto (por ejemplo, $x_0=0.5$). Observa cómo la aproximación mejora rápidamente cuando aumentas el número de iteraciones (por ejemplo, $N=1,2,3...$)
• Busca una segunda raíz: ¿qué pasa si tomas inicializaciones positivas? ¿y si las tomas negativas? ¿Cuántas raíces tiene, aparentemente, la función? Para saberlo de forma rigurosa, podríamos recurrir al análisis matemático, crecimiento, decrecimiento, Teorema de Bolzano, etc, pero este no es el tema que ahora nos ocupa.
• Para esta segunda raíz, observa que basta una cantidad relativamente pequeña de iteraciones para obtener $f(x) \simeq 0$ con una aproximación del orden de $10^{-16}$. Y a partir de ese momento, el valor de $f(x)$ no decrece, por muchas iteraciones que realicemos. El motivo es que el valor 2.22e-16 es el épsilon de la máquina (en doble precisión). En este sentido, $10^{-16}$ «es igual a cero» en el estándar en coma flotante de doble precisión.
• Pero, ¿por qué doble precisión? ¿qué ocurre si hacemos las cuentas en simple precisión? Haz la prueba: tendrás que cambiar el tipo de datos double por float (coma flotante en simple precisión). También el formato lf (long float) por f (float). ¿Coinciden los datos con el épsilon de la máquina en simple precisión, especificado en Wikipedia?

Chiste malo:

- Por supuesto, las matemáticas son una ciencia exacta.

- Entonces, $10^{-16}\neq 0$.

- Depende... 😂